CyclesAndColorings CYCLECOL

All submissions for this problem are available.You are given a connected undirected graph G = (V,E). We define a simple cycle to be $Good$, if it consists of an odd number of edges, and if on deleting all those edges, the graph still remains connected. Note that we do not delete any vertices.

A $4 - Coloring$ of the graph is an assignment of colors to the vertices of the graph and which satisfies these properties:

• Every vertex should be assigned exactly 1 color.
• You can only use one of four colours: {1,2,3,4}.
• There should be no edge$(u,v)$ such that both $u$ and $v$ have been assigned the same color.

You should either find and output a $Good$ cycle, or give a $4 - Coloring$ of the entire graph. Note that the given graph might both of these and multiple instances of these. Any one of them can be printed. Also, you can prove that you can never have a graph which has neither of these.

###Input

The first line of the input contains a single integer, $T$. This denotes the number of testcases.

The first line of each testcase contains two integers: $N$ and $M$, which denote the number of vertices and edges in the graph. The vertices are numbered from $1$ to $N$.

Each of the next $M$ lines contains two integers, $u$ and $v$, denoting that there is an edge between the nodes $u$ and $v$.

###Output

The first line of each testcase’s output should contain a single integer: 1 if you are going to print a $4 − Coloring$, and 2 if you are going to print a $Good$ cycle.

If you had printed 1 in the previous line, then the second line should contain $N$ space separated integers, each of which is one of {1, 2, 3, 4}. The i-th of these numbers should denote the color assigned to Node i in your $4 − Coloring$.

If you had printed 2 in the previous line, then first print the length of the $Good$ cycle in the second line, and print the vertices in the cycle in order in the same line.

###Constraints

• $1 \leq T \leq 5$
• $1 \leq N \leq 10^5$
• $1 \leq M \leq 200000$
• $1 \leq u,v \leq N$
• The graph will not contain multi edges or self-loops.

###Subtasks:

Subtask 1 (9 Points) :

• $M = N$

  Subtask 2 (91 Points) :

• No further constraints.

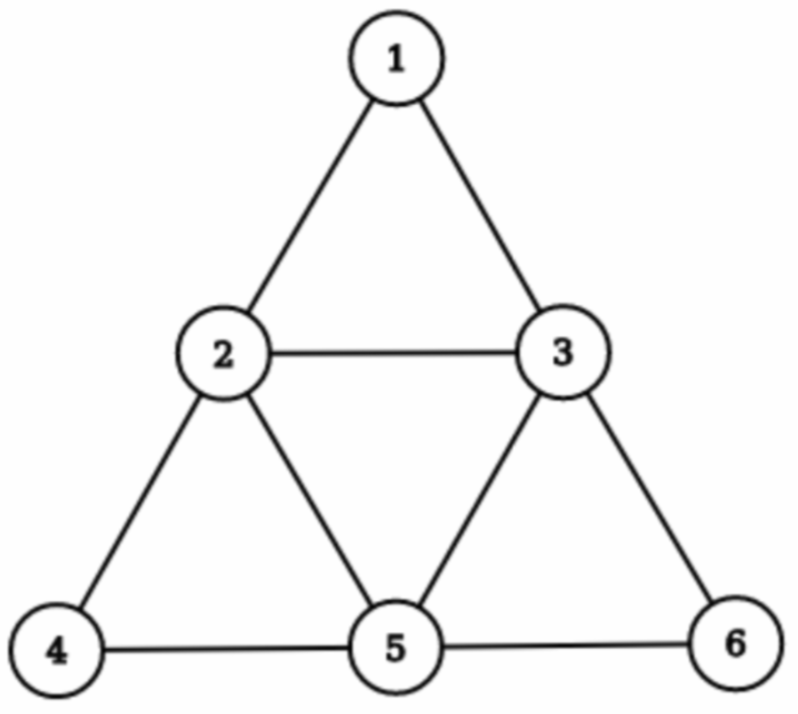
###Sample Input 1: 1 6 9 1 2 1 3 2 3 2 4 5 2 3 5 6 5 3 6 4 5

###Sample Output 1 2 3 5 2 3

###Sample Input 2 1 6 9 1 2 1 3 2 3 2 4 5 2 3 5 6 5 3 6 4 5

###Sample Output 2 1 1 2 3 3 1 4

###Explanation

Explanation 1 : The graph is as follows

2-3-4 forms an odd cycle, and after deleting these three edges, the entire graph still remains connected. Hence we have outputted a $Good$ cycle.

Explanation 2 : The graph is same as before. The colors that we have assigned form a $4 - Coloring$.